General data analysis projects

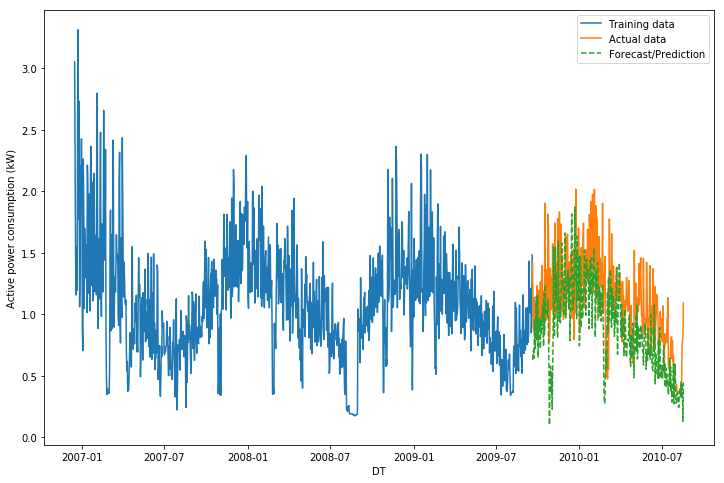
Time Series Analysis and Forecasting using Decomposition

Notebook: Jupyter Notebook
Dataset: Electric power consumption (UCI Machine Learning Repository)
Description: Univariate time-series analysis using Fourier (spectrum) and decomposition-based approaches to forecasting. The notebook also dives into the concepts of stationarity in the context of time-series
Methods/concepts: time-series analysis, Fourier analysis, series decomposition, EDA (exploratory data analysis), stationarity, forecasting, Augmented Dickey-Fuller tests

Deep learning projects

MNIST Digit Recognition using a multilayer perceptron (feed-forward neural network)

Notebook: Jupyter Notebook
Dataset: MNIST database
Description: Implementation of a feed-forward neural network using Tensorflow. The model is trained and tested on the MNIST dataset (pretty much a pre-requisite for training deep learning models).
Methods/concepts: tensorflow, OCR (Optical Character Recognition), EDA (exploratory data analysis), neural network

Modelling of Physical Processes

Least squares regression using harmonic functions

Notebook: Jupyter Notebook
Dataset: Government of Canada - Historical Climate Data
Description: Produces a least squares regression model by fitting a 9-parameter harmonic (trigonometric) function. This regression fits the minimum and maximum temperature data measured at the International Edmonton Airport between 1963 and 1993. Notebook covers pre-processing steps of the data and implementation of the model.
Methods/concepts: least squares regression, harmonic functions, periodicity modelling

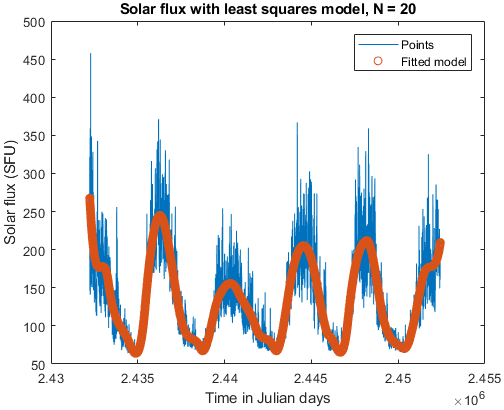
Least squares regression using compact-support basis functions

Notebook: Jupyter Notebook
Dataset: Solar 2000 Model
Description: Produces a least squares regression model by fitting pre-defined basis functions (a piecewise cubic polynomial). This model uses solar flux data ( was generated such that the output as well as its first derivative is fitted exactly, preventing unwanted oscillations generated by sharp variations in the data.
Methods/concepts: least squares regression, basis functions, compact support

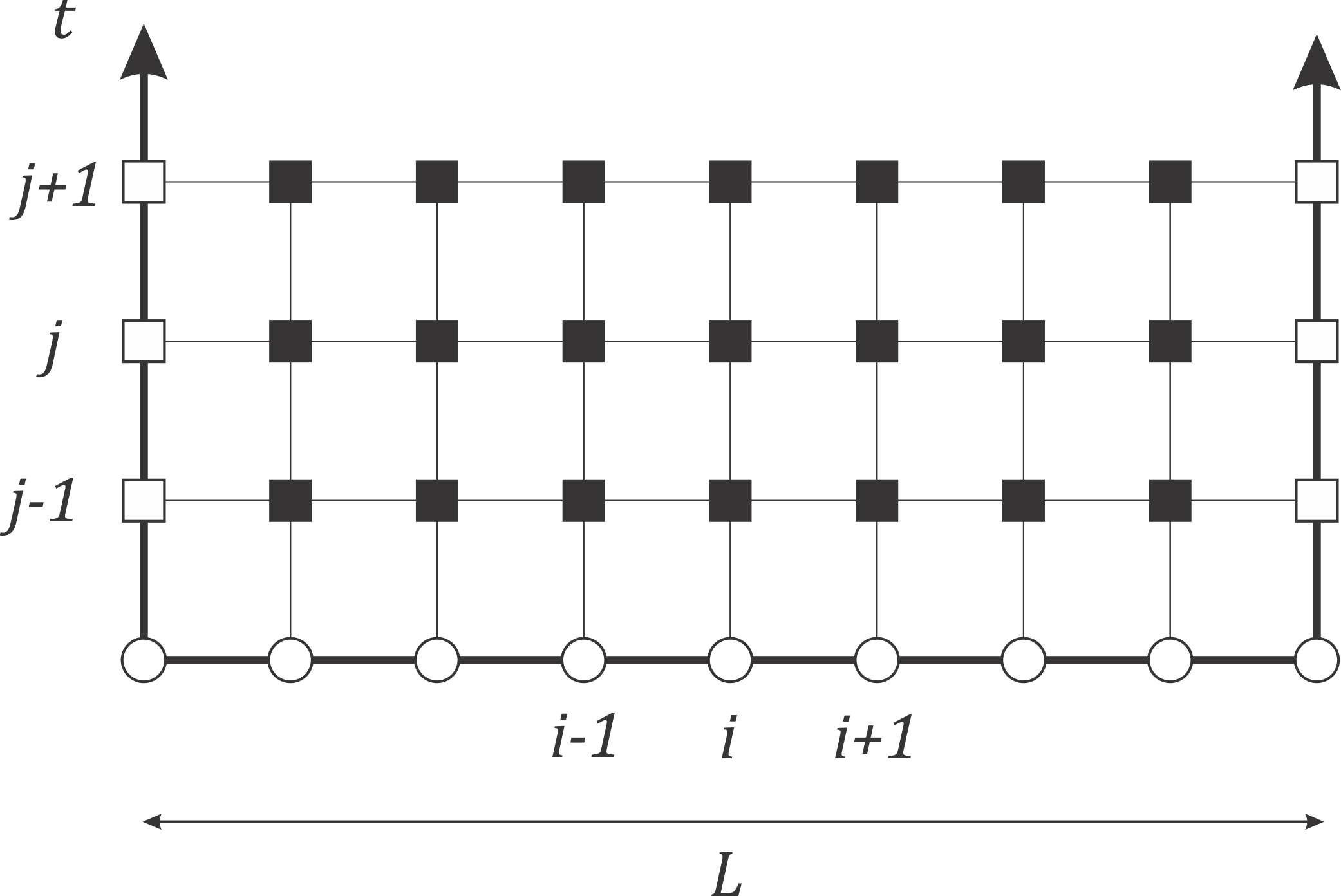
Review of finite-difference schemes for the heat-diffusion equation

Paper: [PDF]
Description: The heat-diffusion equation is a second-order partial differential equation that governs the distribution of heat or diffusing material. This paper reviews some of the many finite-approximation schemes using for solving this equation and provides comparisons on their accuracy and stability.
Methods/concepts: finite-difference, temperature modelling, stability analysis, eigenvalue solutions